|
Kirchhoff's-law-Johnson-(like)-noise
(KLJN)
secure key distribution
Unconditionally (information
theoretically) secure key exchange scheme
based on enhanced Johnson-noise, the
Second Law of Thermodynamics and
Kirchhoff's Law.
The last update in this page below is from
November 14, 2014. A new KLJN page with the updates and the latest hot
news is coming during the Fall of 2016.
Until then, check the Publication List (sections C-D-E)
for news:
http://www.ece.tamu.edu/~noise/publist.pdf
=================================================================================================================
Up to November 14, 2014:
- We identified the experimental error leading to
the giant information leak in the Gunn-Allison-Abbott (GAA) attack, see the next paragraph below. It
is a fundamental error of engineering design. For the huge information
leak results, they use a commercial cable attenuator, which is a voltage
divider (T-element) breaking the single Kirchhoff-loop of the KLJN
system into two coupled loops. Thus, what they measured was not a KLJN
system. Another flaw in a Nature-based journal! Note: a fully built KLJN
would not have been able to function due its built-in current/voltage
comparison units at the two ends. Here is the link to the pdf file of
our critical paper with these details (accepted for publication). click
here.
- The Gunn-Allison-Abbott (GAA) attack is published in (Nature) Scientific Reports. They also tested our breakthrough solution below (see the Entropy
paper) and found that it protected even against their attack, see
Equation (19) and the text around it. Note, they incorrectly say that
alpha must be measured because all the resistors and the line parameters
are public information in the KLJN system, and Alice and Bob knows them
anyway. Concerning the rest of the GAA paper, all our former objections against
the GAA attack holds, see those papers below. To read their Nature
paper, click here.
- Breakthrough:
The famous old (Bergou)-Scheuer-Yariv wire resistance attack (for its
correct treatment, see paper 13 below) is totally eliminated now. The
new defense method, which is to increase the noise temperature of the
smaller resistances, nullifies not only the (Bergou)-Scheuer-Yariv
attack, but totally eliminates also the new, more efficient Second Law
attack. Accepted for publication in Entropy. Click here for the paper.
- Zoltan Gingl
and Robert Mingesz gave a mathematical security proof showing that only
Gaussian noises can be applied in the KLJN system, like it is in the
original Johnson noise based scheme (resistor thermal noise without
extra generators). PloS ONE (2014 April), Click here to read the paper
- Criticism-2 of the GAA attack paper. Due to the incorrect math/physics foundations of the Gunn-Allison-Abbott (GAA) attack system, we carried out the correct analysis proving that
it does not offer anything more efficient than the old comparison
between the mean-square voltages at the cable ends, see the Kish-Scheuer
paper below, in this page. We identified some of the possible
experimental artifacts in GAA's work that could lead to the unphysical
results. Our treatment shows that parasitic deterministic currents in
the loop, non-Gaussianity, aliasing effects, non-linearities, etc, can
affect the security practical KLJN systems if their design is poor. This paper is published. Click here to read the paper.
- Criticism-1 of the GAA attack paper.
Proof that, in
accordance with several laws of physics, no waves exist in a short
cable at low frequencies. Note, this discussion is mostly irrelevant for
security however concludes a historical open question. The paper
was motivated by the opposite claim in the GAA attack manuscript. This
paper
is published. Click here to read the paper.
- Our response to the Bennett-Riedel
manuscript is published in PLOS ONE, click
here
- The most
general
security proof based on the foundation of classical physics: the
continuity of functions describing stable classical physical systems.
With Claes Granqvist, published in Quantum Information Processing as invited paper, click here for the preprint and find the journal version by clicking on the DOI link there.
- Yessica:
Efficient reduction of the bit error probability (10^-12 or less at
practical conditions) with combined current and voltage monitoring, accepted for publication in Journal of Computational Electronics, click
here
- Yessica: Error
probability decays
exponentially with
increasing bandwidth or
bit exchange duration, accepted for publication in PLOS ONE, click
here
Earlier news:
-
Elias:
Unconditionally secure Smart Grid
(electrical power distribution), PLOS ONE, 2013,
click
here
- Physical Uncloneable Function (PUF) Non-Counterfeitable
Hardware Keys, FNL, in press, click
here
- April 16, 2013. After
one year that we had requested it, the Kish
cypher Wikipedia page has been deleted,
see our supporting
comments at the Wikipedia Talk page,
which finally triggered the deletion
action. click here
- Seven new KLJN systems with strongly enhanced
security and transient protocol for the
non-ideal situations click here
Wikipedia disclaimer:
Up
to April 16th, 2013, there was a
Wikipedia site called "Kish cypher",
where even the name "Kish cypher" was
incorrect because this scheme is
not a cypher but a secure key exchange
protocol built on a specific physical
system and its laws. That wiki page got
fortunately deleted but its various versions are still circulating on
the web and in wiki-based books. It was apparent
that many of the contributors either
have not read the papers or have not
been able to follow them. Inspired by
these events, a book
shall be completed and published by World
Scientific (expected at the end of 2014):
Relevant: on August 26, 2013, Scholarpedia published a brief introduction on KLJN click here
<>
<>
Image of
the simplified scheme in the
Swedish magazine Ny Teknik (New Technology)
click to see/enlarge:
The fully protected KLJN
scheme:
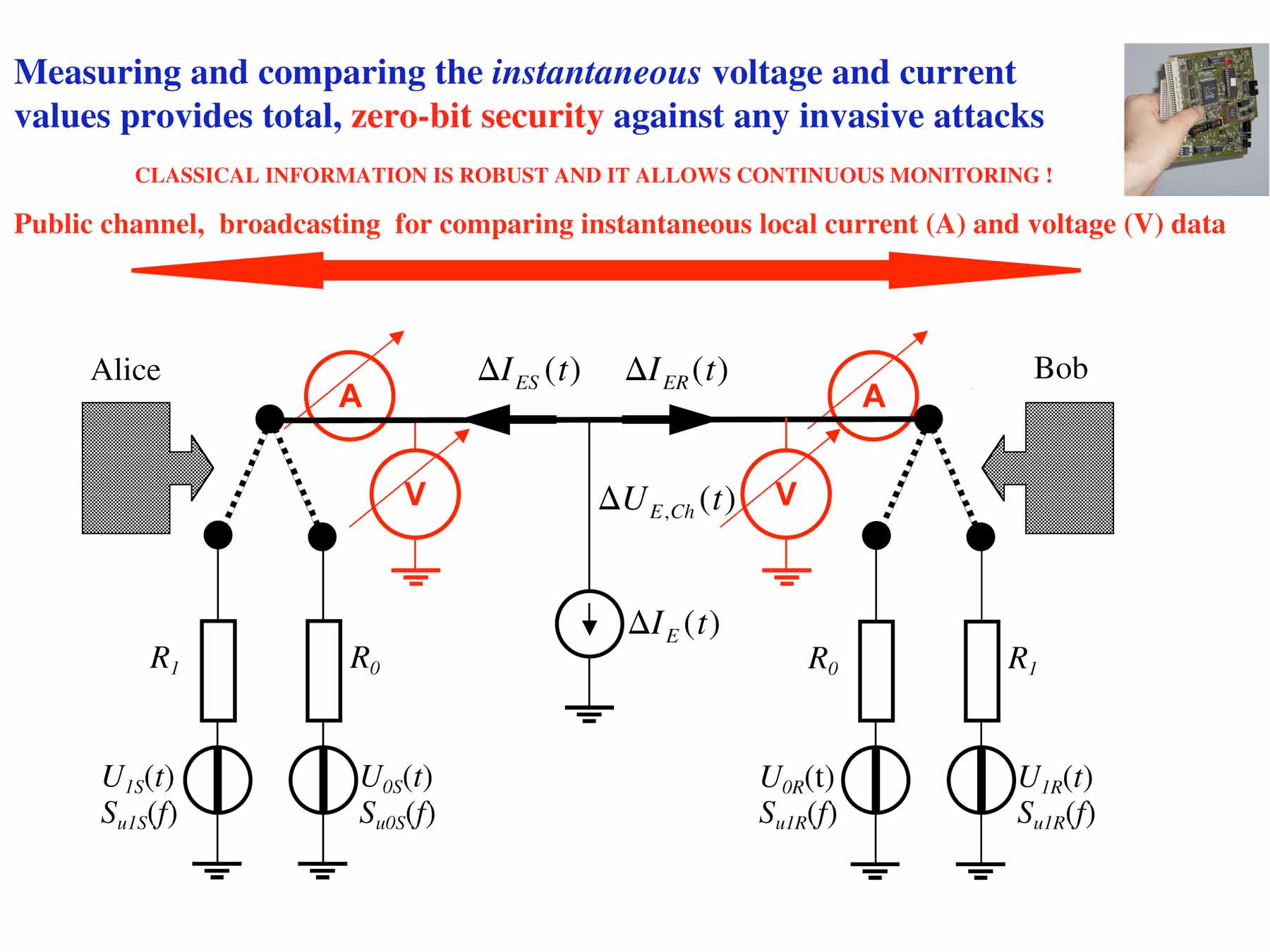
|
|
- Status of the idealistic circuit scheme: Perfect
security [16], Information theoretic level, that
is, the security level is unconditional [16];
Security proofs for idealistic and various
non-idealistic situations are given in papers
[2,3,4,7,10,13,14].
- Status of the practical (non-idealistic)
system. Without further
defense: Imperfect security [16] (same as quantum
encryption) but still Information theoretic [16]
that is, unconditional security level;
Security proofs for idealistic and various
non-idealistic situations are given in papers
[2,3,4,7,10,13,14].
Hacking is
partially possible, (similar to Quantum
Hacking, click to
watch video)
BUT:
- Privacy amplification can
effectively remove the information leak [14]
- Even before privacy
amplification, Alice and Bob has full control of
the amount of information leak [10]
- They can discard the
compromised bits, if necessary [10].
- Thus they are in the
position to discard or manipulate the information
Eve has [10].
- This is a new situation in physical cryptography
and poses deep questions about the best policy for
Alice and Bob. See below the remarks about
information leak and, for a mathematical security
analysis by Tamas Horvath, in the last section of
paper [10] and in paper [14].
- Some of the (other) unique properties of
this secure key exchange scheme:
- Foundation of
the security: The second law of thermodynamics: the
impossibility to construct a perpetual motion
machine of the second kind [2].
- Natural
immunity against the man-in-the-middle-attack [3].
- Information
leak via hacking are miniscule [7] and it is under
full control by Alice and Bob who knows all the
bits that Eve may have correctly extracted [10].
This property is very different from quantum
communicator characteristics and it is only
possible in classical physics
- Privacy amplification can always effectively
remove the information leak and Perfect Security
can be achieved even in non-idealistic system, see
paper [14] below. This is due to the
extraordinary fidelity of the communication.
- Power lines and household power distribution
networks can be utilized for (computationally) unconditional security,
see paper [15] below.
Thus, all the households can be connected in a
chain-like unconditionally secure network with a
key-teleportation technology, see paper [4].
-
Inexpensive, small, robust, low power consumption
and it can be integrated on
computer chips to unconditionally secure the
information within computers, computer games, and
hardware, see paper [11] click here.
Papers:
19. Elias Gonzalez, Laszlo
B. Kish, Robert Balog, Prasad Enjeti, "
Information theoretically secure, enhanced
Johnson noise based key distribution over the
smart grid with switched filters", submitted for
publication, Click
here to read it.
18. L.B. Kish, "Enhanced Secure
Key Exchange Systems Based on the Johnson-Noise
Scheme", accepted for publication. Click here to read
it.
17. R.
Mingesz, L.B. Kish, Z. Gingl, C.G.
Granqvist, H. Wen, F. Peper, T. Eubanks, G.
Schmera, "Unconditional security by the laws
of classical physics",
Metrol. Meas. Syst., Vol. XX (2013), No. 1,
pp. 3–16, open access, Click here to
read it.
16. R. Mingesz, L.B. Kish, Z. Gingl,
C.G. Granqvist, H. Wen, F. Peper, T. Eubanks, G.
Schmera, "Information theoretic security by the
laws of classical physics", Plenary Talk at the
5th IEEE Workshop on Soft Computing Applications,
22-24 August (2012).
15. L.B. Kish,
F. Pepper, "Information Networks Secured by the
Laws of Physics", IEICE Transactions on Communinations
E95-B
(2012) 1501-1507; invited survey paper; includes
the utilization of powerlines, phone landlines and
interet wire lines to build robust secure networks
with information theoretic (unconditional)
security mesures. Click here to read it.
14. T.
Horvath, L.B. Kish, J. Scheuer, "Effective
Privacy Amplification for Secure Classical
Communications", EPL (former Europhysics
Letters)
94 (2011) 28002-p1 - 28002-p6. Click here to
read it.


Left to
right: Robert Mingesz, Laszlo Kish, Zoltan
Gingl at the University of Szeged, Hungary, 12/15/2006; After
the successful experimental demo of the Szegedin
Whisper Project testing
all known breaking attemps, including the
man-in-the-middle attack during the very first run
(quantum encryption is vulnerable against such),
and thus proving superior-to-quantum security.
<><><>
|